Jour et nuit aux solstices et équinoxes

La compréhension habituelle du mécanisme des saisons (voir à "Les saisons") entraîne l'idée simple que la longueur du jour et de la nuit sont égales aux équinoxes et que la longueur du jour décroît jusqu'à un minimum au moment du solstice d'hiver alors que la durée des nuits s'accroît, au contraire, au moment du solstice d'été. Cela, de façon générale, est vrai. Une vue plus détaillée, cependant, permet de nuancer: certains éléments, en effet, font que les jours, aux équinoxes, sont en fait plus longs que les nuits et que, au moment des solstices, la façon dont varie la longueur du jour ou de la nuit nécessite d'être nuancée

Les jours sont plus longs que les nuits à l'équinoxe

La variation de la longueur du jour -ou de la nuit- n'est pas proportionnelle au moment des solstices

Les jours sont plus longs que les nuits à l'équinoxe

Pour les éphémérides, les moments du lever et du coucher du Soleil sont définis comme les moments où le bord meneur ("leading edge"; bord supérieur) -ou le bord suiveur ("trailing edge"; bord inférieur)- du Soleil coupe l'horizon, en montée -ou en descente. On y ajoute la valeur de la diffraction atmosphérique (qui est la modification optique du chemin de la lumière ayant comme conséquence que le Soleil est visible avant -et après- qu'il ne se soit réellement levé -ou couché). La valeur de la diffraction est de 34" et le demi-diamètre du Soleil est de 16". Aussi, la durée réelle du jour un jour donné est en fait plus grande que la durée qui est donnée par les éphémérides: la durée supplémentaire du jour correspond au temps qu'il faut au Soleil pour se déplacer de 100" ((34" + 16") x 2) en élévation le jour en question

La première conséquence de ce constat est que, d'une façon générale, chaque jour de l'année, la durée du jour est toujours, en fait, plus longue que celle de la nuit, contrairement à ce que l'on peut déduire des éphémérides: le Soleil est vu avant le temps -et après, le soir- donné par les éphémérides pour son lever et son coucher. Cela est donc vrai aussi pour les équinoxes: la différence de la longueur du jour par rapport à la valeur donnée par les éphémérides varie en fonction de la latitude du lieu de l'observateur; le plus le lieu d'observation est élevé en latitude -Nord ou Sud- le plus l'angle que fait l'écliptique par rapport à l'horizon, au moment du lever ou du coucher du Soleil, est, en effet, petit et donc le plus la longueur du jour supplémentaire est importante (puisque, du fait de cet angle faible de l'écliptique sur l'horizon, le Soleil met plus de temps pour se lever -ou se coucher- complètement)

De façon pratique, les conséquences de cela sont que, le jour de l'équinoxe, le jour n'est pas égal à la nuit et que c'est avant ou après l'équinoxe que cette égalité a réellement lieu. Quels sont les chiffres? A une latitude de 25° Nord ou Sud, le jour, le jour de l'équinoxe -de printemps ou d'automne- est plus long, en fait, que la nuit, de 8 minutes. La valeur est de 11 mn aux latitudes moyennes et elle atteint 22 mn à 60° de latitude Nord ou Sud. Même à l'équateur, on peut constater une différence de plusieurs minutes. Pour ce qui est de quand la longueur du jour est réellement égale à la nuit, cela a lieu, pour l'hémisphère nord, au printemps, avant l'équinoxe (qui est habituellement vers le 21 mars) et, à l'automne, après celui-ci (qui a habituellement lieu vers le 21 septembre); et le contraire dans l'hémisphère sud. A une latitude de 5° Nord, par exemple, la vraie égalité entre la longueur du jour et de la nuit a lieu vers le 25 février, au printemps et vers le 15 octobre à l'automne soit un décalage de presqu'un mois. Aux latitudes moyennes, le décalage est moindre: l'égalite jour-nuit a lieu vers le 17 mars et le 26 septembre, soit avec une différence de 4 ou 5 jours par rapport à l'équinoxe

La variation de la longueur du jour -ou de la nuit- n'est pas proportionnelle au moment des solstices

La question des solstices, maintenant. Le fait incontestable, pour ces deux moments de l'année -le solstice d'été et le solstice d'hiver- est que, le jour du solstice d'hiver (habituellement le 21 décembre), l'observateur notera que c'est le jour où la durée du jour est la plus courte et que, le jour du solstice d'été (habituellement le 21 juin), il notera que c'est le jour où c'est la durée de la nuit qui est la plus courte (cela est vrai pour l'hémisphère nord comme pour l'hémisphère sud mais, bien sûr, de façon inversée). La nuance qu'il faut apporter concerne les temps du lever et du coucher du Soleil avant et après le solstice. La façon dont ils évoluent n'est pas en proportion, c'est-à-dire que, si cette évolution se faisait en proportion -en prenant l'exemple du solstice d'hiver dans l'hémisphère nord- elle se ferait en ce sens que le lever du Soleil devrait avoir lieu de plus en plus tard, chaque jour, au fur et à mesure que l'on se rapproche de la date du solstice , et, chaque jour, le coucher du Soleil aurait lieu de plus en plus tôt. Puis l'inverse après le solstice (le Soleil recommencerait à se lever de plus en plus tôt au fur et à mesure que l'on s'éloignerait du solstice, et à se coucher de plus en plus tard). Cette proportion, en fait, n'est pas respectée! Et elle ne l'est pas du fait d'un effet combiné de la position de la Terre sur son orbite et du phénomène que l'on appelle l'"équation du temps"

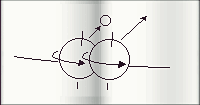jour solaire: il faut que la Terre tourne un peu plus sur elle-même pour que le Soleil, chaque jour, se retrouve à la même position apparente par rapport à l'observateur

L'"équation du temps" est un phénomène lié au concept de "jour solaire". Le "jour solaire", en astronomie, est le temps qui s'écoule entre deux passages du Soleil au méridien de l'observateur, c'est-à-dire au Sud de celui-ci. Mais, en une journée, la Terre a avancé sur son orbite; aussi, chaque jour, le Soleil, après un jour, se trouve en fait légèrement plus à l'Est du Sud de l'observateur. Chaque jour, il faut que la Terre tourne de 4 minutes de plus sur elle-même (1° sur le ciel) pour que l'observateur voie le Soleil revenu au méridien. Allons plus avant: ce décalage de 4 mn n'est pas stable au long de l'année et cela est dû à deux facteurs, qui sont la configuration de l'orbite terrestre et la relation entre l'écliptique et l'équateur céleste au cours de l'année. L'orbite de la Terre, en effet, n'est pas un cercle mais une ellipse. Selon la seconde loi de Képler (des aires égales sont parcourues en des temps égaux), cela a comme conséquence qu'à à un endroit de l'orbite, la Terre accélère (cela a lieu au périhélie -le point de l'orbite où la Terre est au plus près du Soleil, habituellement au mois de janvier) et qu'à à un autre endroit (à l'aphélie -le point de l'orbite où la Terre est au plus loin du Soleil, habituellement en juillet) elle ralentit. Pour ce qui est de la relation entre l'écliptique -le plan moyen, vu de la Terre, du système solaire ou, ce qui revient au même, le chemin apparent du Soleil, du fait de la rotation de la Terre sur l'orbite, sur la sphère céleste- et l'équateur céleste -la projection, sur la sphère céleste, de l'équateur terrestre- le déplacement de la Terre sur l'orbite a comme conséquence qu'aux solstices, l'écliptique est vu parallèle à l'équateur céleste -en haut ou en bas de celui-ci- et, qu'aux équinoxes, par contre, il fait un angle (le Soleil traversant l'équateur céleste en montée ou en descente). La conséquence de cela est, qu'aux solstices, le Soleil semble se déplacer plus lentement, dans le ciel, par rapport au fond des constellations, qu'au moment des équinoxes

l'équation du temps au long de l'année

Ce sont donc deux éléments, la notion de jour solaire et la vitesse différente de la Terre selon sa position sur son orbite ainsi que la relation entre l'écliptique et l'équateur céleste, qui sont à l'origine de l'"équation du temps": le décalage de 4 mn qu'induit, chaque jour, le concept de jour solaire n'est pas stable au long de l'année; le Soleil, selon le moment de l'année, sera, par rapport au midi de la montre de l'observateur, en retard d'une valeur variable et, à certaines périodes de l'année, ce retard se transformera même en avance. On appelle donc équation du temps le décalage vrai, pour un jour donné, entre le jour solaire et le midi à la montre de l'observateur ou, ce qui est l'équivalent, entre le moment où le Soleil passe au méridien de l'observateur et le midi à sa montre. Le Soleil est en retard par rapport au midi de l'observateur entre aux alentours de la dernière semaine de décembre jusque vers la mi-avril, et de mi-juin jusqu'à la dernière semaine d'août; et il est en avance de mi-avril à mi-juin, et de la dernière semaine d'août à la dernière semaine de décembre. La valeur de la différence (en moins, ou en plus) varie, pour les périodes dernière semaine de décembre/mi-avril et dernière semaine d'août-dernière semaine de décembre, entre 0 et jusqu'à 15 à 16 mn et, pour les périodes mi-juin/dernière semaine d'août et mi-avril/mi-juin, entre 0 et 4 à 6 mn

Quelle est donc l'impact de l'équation du temps en terme des proportions selon lesquelles la durée du jour varie avant et après les solstices? On doit d'abord considérer que le mécanisme des saisons -qui est déterminé par là où la Terre se trouve sur son orbite- reste ce qui détermine en premier lieu l'heure à laquelle le Soleil se lève et se couche chaque jour: lorsque l'on avance vers le solstice d'hiver, par exemple, le Soleil, d'une façon générale, se lève de plus en plus tard et se couche de plus en plus tôt puis l'inverse après le solstice: le Soleil, d'une façon générale se lève alors de plus en plus tôt, et se couche de plus en plus tard. Mais intervient alors l'équation du temps. L'équation du temps, on l'a vu, fait que le Soleil, au midi de la montre de l'observateur est soit en retard, soit en avance. Aussi, lorsque le Soleil est en retard au midi vrai de l'observateur, cela signifie aussi qu'il s'est levé plus tard (et qu'il se couchera plus tard aussi)! Aussi, l'évolution progressive du lever et du coucher du Soleil lorsque l'on marche au solstice d'hiver, qui devrait, du seul fait du mécanisme des saisons, se faire de façon régulière, est perturbée par l'équation du temps. Ainsi, pour l'hémisphère nord et le solstice d'hiver, on note que l'équation du temps fait que le coucher du Soleil, jusqu'au solstice même, est "accru"; il a lieu plus tard (alors qu'il devrait avoir lieu plus tôt). Alors que le lever du Soleil, lui, est "freiné"; il a lieu plus tôt (alors qu'il devrait avoir lieu plus tard). Et la conséquence inverse a lieu après le solstice: la tendance qu'aurait le Soleil à alors se lever plus tôt est freinée (le Soleil continue de se lever tard) alors que, dans le même moment, la tendance qu'il a à se coucher plus tard est accentuée (le Soleil évolue rapidement vers des couchers de plus en plus tardifs). Ainsi, la date à laquelle le Soleil se couche le plus tôt a lieu dès le 8 décembre -soit presque deux semaines avant le solstice d'hiver- alors que la date à laquelle le Soleil se lève le plus tard a lieu, elle, le 5 janvier (soit quinze jours après le solstice). Les mêmes modifications se retrouvent pour le solstice d'été mais, du fait des valeurs de l'équation du temps, elles ne sont pas aussi importantes: ainsi, pour une latitude Nord de 40°, la date à laquelle le Soleil se lève le plus tôt a lieu le 14 juin -une semaine avant le solstice- et la date à laquelle il se couche le plus tard a lieu le 28 juin -une semaine après. Si l'on envisage l'influence de l'équation du temps d'une façon encore plus générale, on pourra constater qu'elle accroît ainsi le nombre de jours où le jour est court en hiver -rendant l'hiver plus hivernal- mais qu'elle accroît aussi, pour l'été, le nombre de jours au cours desquels les nuits sont courtes -accentuant cette impression des longs crépuscules de l'été. Enfin, pour conclure, on notera que l'équation du temps est également le phénomène qui est responsable de ce que l'on appelle un "analemne", le fait que, si l'on note -ou photographie (ATTENTION, Soleil, DANGER! voir notre page spéciale sur les DANGERS DE L'OBSERVATION SOLAIRE)- la position du Soleil, chaque jour, depuis une même position de l'observateur, on obtient une courbe en forme de 8. On utilise cette notion d'analemne pour constuire les cadrans solaires