Theory Lagrangian Points

The famous so-called Lagrangian points are a two-celestial body system particular points, one body being neatly much heavier than the other. Gravitational attractions exerted by these two bodies on a lighter third are in equilibrium for five points, which are said Lagrangian points, from Joseph-Louis Lagrange, a 18th century Italian-born French mathematician and astronome (1736-1813) who studied the "three-body problem" (so-called because three bodies are orbiting each other) for the Earth, Sun, and Moon in 1764, and by 1772 he had found the solution; there are five stable points at which you could put an object and have it stay fixed in place relative to the other two. Putting a spacecraft at any of these points allows it to stay in a fixed position relative to the Earth and Sun. At L2, for example, a object almost a million miles farther out from the sun should move more slowly, taking more than a year to complete its orbit around the sun. However, at L2, exactly lined up with both the sun and Earth, the added gravity of the two large bodies pulling in the same direction gives a spacecraft an extra boost of energy, locking it into perfect unison with the Earth's yearly orbit. Lagrangian points apply to any body, and to artificial satellites as well as asteroids. Even more generally they apply too to a solar system gravitational tugs comprehensive view. For each two-body system, there are 5 Lagrangian points. note: this text is the same than the one found in the "Tutorials About Space" section

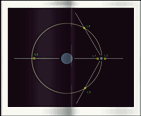click to a diagram of the Lagrangian points

Lagrangian points' gravitational explanation is based on Kepler's Third Law: the nearer a body orbits another body, the faster it moves. Five Lagrangian points are points where gravitational tugs either curbs or accentuates the law however. Lagrangian points are also called libration points. At the first Lagrangian point (L1), an object should orbit the Sun faster than Earth, as nearer to the Sun; but Earth's gravitational attraction partly cancels Sun's and the object moves slower -at the same speed than Earth indeed, orbiting the Sun in 1 year

Spacecraft may hang and stay at a Lagrangian point. They may too orbit it along what is termed an halo orbit a orbit with its center at the Lagrangian point. The solar probe Soho is in one of these orbits around Sun-Earth L1. Next generation James Webb Telescope should be positionned at L2. L1 may be chosen for observing the Sun, as L2, being on Earth's far side, is better for infrared observations. L4 and L5 are famous in the Sun-Jupiter system as they are the places for two swarms of asteroids which orbits along with Jupiter; these asteroids are called Trojans. In the Sun-Earth system L1 is near Earth, 950,000 miles away only; L2 is at about the same distance on the far side of the Earth. L1 and L2 are at the limits of the so-called Hill's sphere, a limit at which Sun and planet's gravity balance each other. Moons may only exist inside this sphere. Beyond, they would be taken away by Sun from the planet; theoretically, retrograde satellites may be hold by the planet's gravity well beyond the Hill's sphere limit. L3 is on the other side of the Sun relatively to Earth, at about the same distance than the Earth. L4 and L5 are at an angle of 60° defined as Earth-Sun L4 or L5

A more advanced use of Lagrangian points relates to space travel, fuel efficiency, and even a comprehensive view of gravitational effects in the solar system. Robert Farquhar, Kathleen Howell and Lo are the founder, and specialists of these questions. Due to the theoretical interconnection between the diverse Lagrangian points of solar and Earth-Moon systems, a craft may be efficiently sent to L1 (the point where is Soho, e.g.), placed in an halo orbit, then brought back Earth, mostly using gravitational tugs at Lagrangian points. Or a planetary probe might efficiently be propulsed by such mean in the near-environment of a gas giant, and so be able to study its moons at a low fuel cost. It seems that such trips might be too long in case of interplanetary probes however. These views are based on the chaos theory, and the n-body problem: as Newton had adressed a two-body orbits problem saying that orbits are always one of three conics, Lagrange found the Lagrangian points as he was addressing the three-body question. Present works are still in this frame: they are trying to find solutions to the three-body problem. They aim too to a comprehensive view of gravitational effects in the solar system. Solar system, in these views, tends to be seen as a complex figure of orbits-defined surfaces (which are termed manifolds)