
| CONTENT - A useful tutorial about the theory of orbits |
Orbit is the path a celestial body describes about another one. As far as solar system is concerned, it is Kepler who first studied scientifically orbits of solar system planets in the 17th century, and it is Newton which through gravity gave the fundamental reason to planets' motion. These theoretical concepts are always valid and may be generally applied to most of celestial objects. From a theoretical point of view, the orbit of a celestial body around a other one nowadays is explained through Einstein's General Theory of Relativity. Spacetime around the main body is curved by the mass of it as the orbiting body is travelling around that curve (the comparison usually used to figure out that concept is the one of a heavy sphere laid down on a elastic fabric; that one is carving under that weight as the orbiting body is a smaller sphere which is orbiting along the slope of the curve)
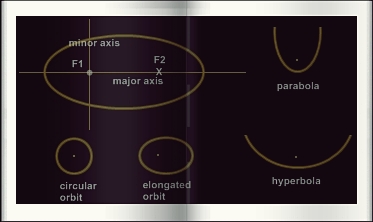
Most of celestial bodies' orbits, like Newton demonstrated, have the form of either of the three possible sections of a cone. A ellipse, a parabola, or a hyperbola. Most however are ellipses, which are 'closed' orbits and with a form of an ovalized circle. Most of solar system planets have elliptical orbits. An orbit may be counterclockwise (orbit is termed direct) or clockwise (retrograde) as seen from the north pole of the ecliptic. All planets of the solar system have a direct motion. An elliptical orbit is a section of cone and has two focii (instead of the one a circle has). An ellipse has two axis: the major axis which intersects the two focii; the minor axis, which is the perpendicular to the previous at the ellipse's center. The semimajor axis of an orbit is the average distance from the orbiting body to the central body. As name tells it is the half of the major axis. Ellipses are diversely elongated relative to a circle shape: elongation of an orbit is described as its eccentricity; it ranges from 0 (the orbit is circular) to > 1 (orbit is an hyperbola). 1 is for a parabola. An elliptical orbit has an eccentricity 0 > e < 1. Technically, eccentricity is the ratio of distance between the foci (d) of the ellipse and the length of the major axis (a): e = d / a. A parabolic orbit is performed when a body has reached what is called its "escape velocity" -the speed which is needed for an orbiting body to leave its orbit around the main body. An hyperbolic orbit occurs whent the orbiting body is moving faster than the escape velocity. An hyperbolic orbit is a more flattened curve than a parabolic one. Period is the amount of time it takes to the body to complete a revolution (revolution is the full length of the orbit)
Orbits of celestial bodies are defined relatively to a plane of reference. In the solar system, this plane is Earth's orbit's. It is called the ecliptic. Inclination is the technical name for the orbit's plane tilt relative to the reference plane; it is the angle between the plane of the orbit of the body and the reference plane (more precisely between the body's axis and a perpendicular drawn from the reference plane, the perpendicular being 0 at its north pole, and the count made left and down to 180 degrees). Nodes are points of the orbit where the body, along its course, crosses, up or down the plane of reference (ascending node is the point where the body crosses plane upwards; descending node is the point where the body crosses downwards). Line intersecting both nodes is called the line of nodes. As most orbits are ellipses, two other points are of importance: apsides, which are the points where the orbiting body is either closer to the central body (this points is said periapsis) or farther of it (apoapsis); for bodies orbiting the Sun, these points are said perihelion and aphelion (from the Greek "helios", Sun); for a body orbiting Earth, perigee and apogee are used. Due to Kepler's second law (equal areas are sweeped in equal amounts of time) a body moves swifter at its peripasis and slower at its apoapsis. Due to the general movement of orbits, lines of nodes and apsides are moving with time (for nodes it is said progression if in the same direction than the orbit, regression otherwise). The line of the apsides of Mercury, as an example, is modifying itself, clockwise, along a timespan of 100,000 years as the move, further, is accelerated by the general relativity, Sun's loss of mass or oblateness, or other planets in the solar system

More technical data may be known about orbits:
 | click to the technical data of an orbit |