
| CONTENU - Tutoriel utile, qui donne l'essentiel des notions qu'il faut connaître en termes d'orbite des corps célestes |
Une orbite, en astronomie, est le chemin qu'un corps céleste parcourt autour d'un autre. En ce qui concerne le système solaire, c'est Képler qui, au XVIIème siècle, étudia scientifiquement, le premier, les orbites des planètes, et c'est Newton qui, par la théorie de la gravitation, expliqua les bases fondamentales de leur mouvement. Ces concepts théoriques sont toujours valables et peuvent être, d'une façon générale, appliqués à la plupart des objets célestes. Sur un plan théorique, l'orbite d'un corps autour d'un autre, de nos jours, s'explique par la Relativité générale: l'espace-temps autour du corps principal est courbé par la masse de celui-ci; le corps orbitant parcourt cette courbure (l'image habituellement donnée pour représenter ce concept est celui d'une sphère lourde posée sur une surface élastique; celle-ci se creuse sous le corps; le corps orbitant est une sphère plus petite qui orbite en suivant la pente de la courbure)
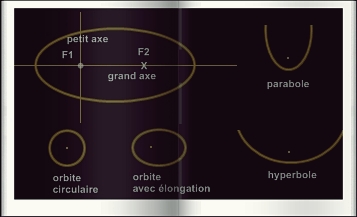
Les orbites des corps célestes, comme l'a démontré Newton peuvent être l'un des trois types de section de cône: une ellipse, une parabole ou une hyperbole. La plupart, cependant, sont des ellipses, c'est-à-dire des orbites fermées, en forme de cercle ovalisé. La plupart des planètes du système solaire, ainsi, ont des orbites elliptiques. Une orbite peut être parcourue, vue depuis au-dessus du pôle nord du corps central (ou pôle nord de l'écliptique), dans le sens contraire des aiguilles d'une montre (on parle d'"orbite directe") ou dans le sens des aiguilles d'une montre ("orbite rétrograde"). Toutes les planètes du système solaire ont des orbites directes. Pour ce qui est du caractère elliptique des orbites, il faut savoir qu'une ellipse est une section de cône et qu'elle a deux foyers (un cercle n'en a qu'un seul). Une ellipse a deux axes: le "grand axe", qui intersecte les deux foyers de l'ellipse; le "petit axe", perpendiculaire au précédent au centre de l'ellipse. Le "demi-grand axe" d'une ellipse, ainsi, est la distance moyenne du corps qui orbite au corps autour duquel il orbite. Comme le nom l'indique, la valeur en est la moitié du grand axe. Les ellipses, par ailleurs, peuvent varier de par rapport à un cercle parfait de différentes valeurs; elles peuvent être diversement "allongées" par rapport à un cercle. Pour ce qui est d'une orbite, cette différence s'appelle l"élongation" de l'orbite et le degré auquel elle diffère d'un cercle, s'appelle l'"excentricité" de l'orbite. L'excentricité d'une orbite varie de 0 (l'orbite est un cercle) à > 1 (l'orbite est une hyperbole). La valeur 1 désigne une parabole. Une orbite elliptique, elle, a une excentricité comprise entre 0 et 1. L'excentricité, techniquement, est le rapport entre la distance entre les foyers (d) de l'ellipse et la valeur du grand axe (e = d / a). Il y a orbite parabolique lorsqu'un corps atteint ce que l'on appelle sa "vitesse d'échappement", la vitesse à laquelle il quitte l'orbite du corps autour duquel il gravite. Il y a orbite hyperbolique, lorsque le corps dépasse la vitesse d'échappement. La courbe d'une telle orbite est plus "aplatie" que celle d'une orbite parabolique. On appelle "période de révolution" le temps qu'il faut au corps céleste pour accomplir une orbite. La "révolution", proprement dit, est la longueur de l'orbite
Les orbites des corps célestes se définissent par rapport à un plan de référence. Dans le système solaire, ce plan est celui de l'orbite de la Terre. On l'appelle l'"écliptique". L'angle (la différence) éventuel du plan d'une orbite par rapport au plan de référence s'appelle l'"inclinaison" (techniquement, l'inclinaison de l'orbite est l'angle entre l'axe des pôles du corps céleste orbitant et une perpendiculaire au plan de référence, le 0 étant au Nord de la perpendiculaire et l'inclinaison étant comptée vers la gauche, jusqu'à 180°). On appelle "noeuds" les points de l'orbite où le corps céleste traverse -en montée ou en descente- le plan de référence. On parle de "noeud ascendant" dans le premier cas et de "noeud descendant" dans le second. La ligne qui joint les deux noeuds de l'orbite s'appelle la "ligne des noeuds". Comme la plupart des orbites sont des ellipses, deux autres points présentent un intérêt: les "apsides". Les apsides sont les deux points de l'orbite où le corps céleste est soit au plus près du corps autour duquel il orbite (on appelle ce point le "périapse" -suffixe grec "peri", près), soit au plus loin de celui-ci ("apoapse" -suffixe grec "apo", loin). Pour les corps qui gravitent autour du Soleil, ces points sont dits "périhélie" et "aphélie" (du grec "helios", Soleil). Pour un corps qui orbite autour de la Terre, on parle de "périgée" et d'"apogée" -du grec "gê", la Terre. Du fait de la seconde loi de Képler (des aires égales du plan d'une orbite sont balayées en un temps égal), un corps en orbite a une vitesse plus élevée à son périapse qu'à son apoapse. On notera que, du fait de l'évolution générale des orbites (par exemple du fait des influences gravitationnelles entre plusieurs corps en orbite autour d'un même centre), la ligne des noeuds et la ligne des apsides "tournent" avec le temps. Pour la ligne des noeuds, on parle de "progression" lorsque le mouvement se fait dans la direction de l'orbite et de "régression" lorsque le mouvement est contraire. La ligne des apsides de Mercure, par exemple -le mouvement, de plus, étant accru par la relativité générale- se modifie sur une période de 100000 ans, dans le sens de la rotation des aiguilles d'une montre (jouent aussi un rôle le perte de masse ou l'aplatissement des pôles du Soleil ainsi que l'influence gravitationnelle des autres planètes du système solaire)

Des données techniques complémentaires peuvent être utiles à la compréhension d'une orbite
 | cliquer vers les données techniques applicables à une orbite |